dignityです！今回は、数IAの二次関数についてです。二次関数は高校数学で一番最初に躓いてしまう単元の一つです。
この記事では、二次関数を解くための必須の思考プロセスを徹底解説します。基本の知識から、最大最小、そして難易度の高い「解の配置」問題まで、なぜその解法を使うのかを理解して、二次関数をあなたの得意単元にしましょう！
二次関数の基本知識
二次関数を初めて勉強するよっていう人にもまず知っててほしい基本知識を押さえましょう
a. 定義
二次関数とは、変数 x と y の関係が y=(二次式) で表される関数です。
- 一般形:
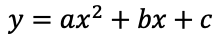（a,b,c は定数で、❌ a=0） - a=0 ではないのが最も重要です。a=0 だと x2 の項が消え、一次関数になってしまうからです。
b. グラフの形：放物線
二次関数のグラフは、放物線と呼ばれるU字型または逆U字型の曲線になります。
- a の符号の役割:
- a>0 のとき：下に凸（∪ の形。開いている方向が上）
- a<0 のとき：上に凸（∩ の形。開いている方向が下）
- どっちに凸かわからなくならないようにしましょう。
- ∣a∣ の大きさの役割:
- グラフをイメージするとわかりやすいですが、xが1増えた時に、大きければ大きいほどyが大きくなりますよね。グラフにして書いてみると、大きくなるほど∣a∣ がグラフの開きは狭くなります。
- 逆に、∣a∣ が小さいほど、グラフの開きは広くなります。
2. 重要な点と線
二次関数のグラフを特徴づける非常に重要な要素が2つあります。
a. 頂点
放物線の最も低い点（a>0 の場合）または最も高い点（a<0 の場合）です。
- 関数の最大値・最小値を考える上で、最も重要となる点です。
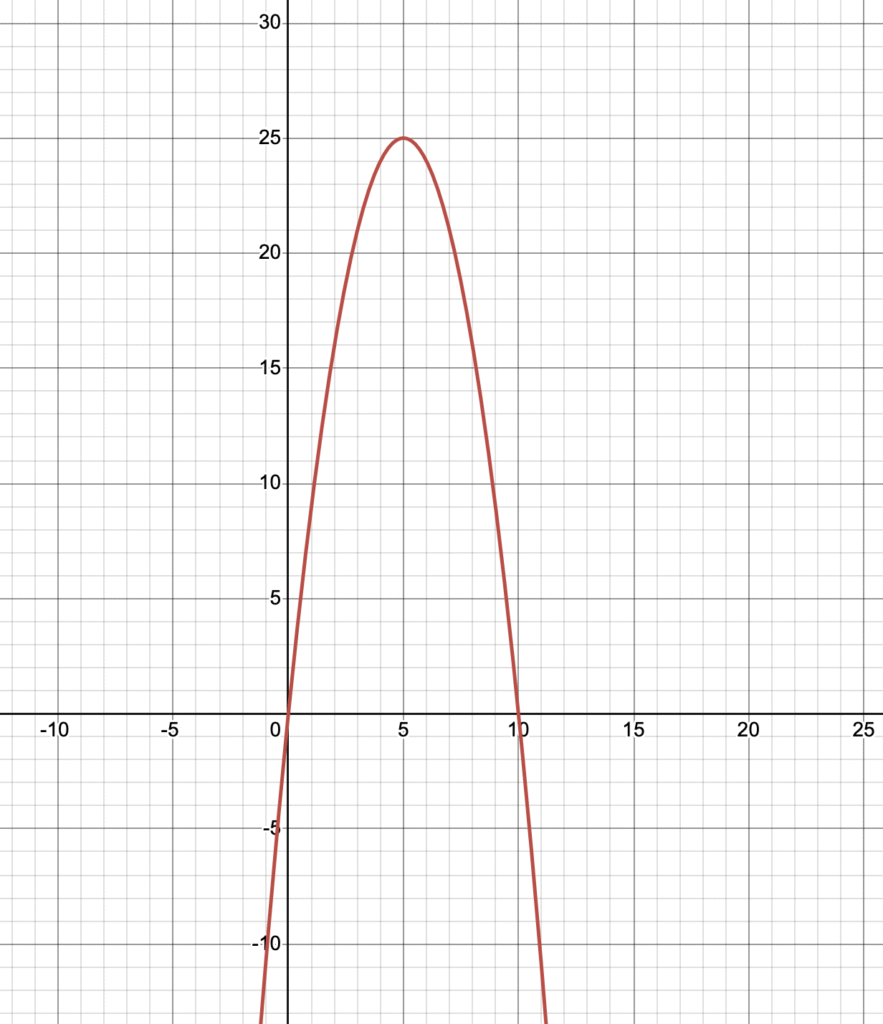
例えば、こんなグラフがあったとしたら最も高い点である（5,25)がこのグラフの頂点であることがわかります。
b. 軸
頂点を通り、y 軸に平行な直線です。
- 放物線は、この軸に関して線対称になっています。
上のグラフの場合だったら、x=5が軸になります。
3. グラフの標準形と平方完成
二次関数の問題を解く上で、一般形からこの標準形に変形することが最も重要な技術となります。
a. 標準形
二次関数の最も便利な形で、頂点の座標が一目でわかります。
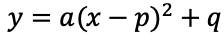
- 標準形の形は上記の式で表されます
- このとき、グラフの頂点の座標は (p,q)、軸の方程式は x=p となります。
注意 (x+p)になっている時は、-pになります。そのまま読み取らないようにしてください。
b. 平方完成
一般形を標準形に変形する作業を平方完成と呼びます。
- これは二次関数の最大・最小、グラフの平行移動、二次方程式の解など、あらゆる問題を解くための必須スキルです。
この計算をすることで、一般形を標準形に変形し、グラフの最も重要な特徴である頂点と軸を求めることができます。
二次関数の対称性（軸）
二次関数の特徴として、頂点にまっすぐな縦線（y軸の直線）を引いた時、必ず左右対称になります。
二次関数は という形で習い始めますが、この**「一般形」からはグラフの見た目、特にその「顔」とも言える頂点がすぐにわかりません。グラフの最も重要な特徴である頂点の座標と軸（対称軸）を知るためには、必ず「平方完成」**という作業が必要です。
二次関数の3つの形式と役割
二次関数には、役割に応じた3つの形式があります。
上から一般式、標準形、因数分解形です。それぞれの役割を表にしてみました。
| 形式 | 何がわかるか（役割） |
| 一般式 | y 切片が (0,c) であることがわかる。 |
| 標準形 | 頂点が (p,q)、軸が x=p であることがわかる（最重要） |
| 因数分解形 | x 軸との交点（解）が α と β であることがわかる。 |
それぞれ問題で何を聞かれているか、何を求めたいかによって使う場面が違うので覚えておきましょう。
絶対に覚えるべき！ 軸の公式
計算を省略したい、または検算したい場合は、軸の公式を必ず暗記しておきましょう。 軸はいつでも
x=−b/2a
で求められます。二次関数を解くためには、「軸」がとても重要です。二次関数の最大最小を求める時に、軸からどのくらい離れているかで判断することが多くあります。なので、軸を二次関数の軸をまず求めようとした時に、この公式で求めることができるのでとても重要です。必ず覚えておきましょう。
2. 範囲で考える！最大値・最小値の決定ルール
二次関数の最大値（Max）や最小値（Min）を求める問題は、「軸」が「定義域（範囲）」の中のどこにあるかだけで決まります。
最大・最小問題を解くときの鉄則は、必ずグラフ（放物線）を書き、範囲と軸の位置関係を図示してから判断することが重要です。
最小値 (Min) を探す → 軸が主役！
最小値は、グラフの「一番低いところ」です。
x^2の係数によって、上に凸のグラフか、下に凸のグラフ化を判断しましょう。
下に凸の場合
- 軸が範囲に含まれている場合：
- 一番低い点はグラフ全体の頂点であるため、最小値は必ず頂点の y 座標になります。
- 軸が範囲から外れている場合：
- 定義域が頂点を含まない場合、最小値は、軸に一番近い方の端点（範囲の端っこ）の y 座標になります。
上に凸の場合
1.軸が範囲に含まれている場合：
- まず与えられた範囲を確認します。
- そしてその範囲が頂点の座標からどのくらい離れているか確認しましょう。
- 頂点からよcり離れている方が最小値になります。（対称性）
軸が範囲から外れている場合：
- これも、頂点の座標からより離れている方が最小値になります。
最大値 (Max) を探す → 端点が主役！
最大値も下に凸の場合と、上に凸の場合で違ってきます。
下に凸の場合
グラフの中で「軸から一番遠いところ」で発生します。グラフは軸に対して対称であるため、軸から離れるほど y 座標は大きくなります。
つまり、最大値は、範囲の「左端」か「右端」のどちらかで決定します。
- 軸が範囲の真ん中よりも左にあれば → 右端が軸から最も遠くなり、最大値になります。
- 軸が範囲の真ん中よりも右にあれば → 左端が軸から最も遠くなり、最大値になります。
- 軸が真ん中と一致していれば → 両端とも最大値になります。
軸を含んでない場合でも、軸から一番遠いところが最大値になります。
上に凸の場合
軸を含んでいる場合、軸が最大値になります。
軸を含んでいない場合は、軸から一番近いところが最大値になります。下に凸と逆なんだなーって覚えておけばいいです。この場面でもグラフを書いてみたらすぐわかりますね。
3. 解の配置問題：3つの条件で交点を追い詰める！
「二次方程式の解が特定の条件（例えば、異なる2つの正の数）を満たすには？」といった、解の符号や位置に関する問題を解の配置問題と呼びます。
これは、二次関数 y=f(x) のグラフと x 軸の交点（解）の位置を求めるために、以下の3つの条件を組み合わせることで解決します。
【解の配置の3つの条件】
| 条件 | 記号 | 意味と考え方 |
| 1. 端点（たんてん） | f(k) | 特定の x の値（例：x=0 や x=1 など）における y 座標の符号（x 軸より上にあるか下にあるか）を調べ、解の位置を制限します。 |
| 2. 軸（じく） | -b/2a | 軸が特定の範囲（例：x>0 や 1<x<3）に含まれるかを調べます。解が対称性を持つために必要です。 |
| 3. 判別式（はんべつしき） | D | 異なる 2 つの解を持つか (D>0)、接するか (D=0) を確定させます。 |
記述の時に使う条件
パターン①：異なる2つの解が正である条件
解が x 軸の正の部分に二つあるためには、以下の3つ全てを満たす必要があります。
- 端点： f(0)>0
- x=0 のとき y 座標が正（x 軸より上）にあることで、解が 0 ではないことを保証します。
- f(0)と簡単に使ってますが、f(0)は、一般式のC(切片）の部分です。
- 軸： −2ab>0
- 軸が y 軸の右側にある（正である）ことで、二つの解が両方とも正であることを保証します。
- 判別式： D>0
- x 軸と異なる 2 点で交わることを保証します。
パターン②：片方の解が正、もう片方の解が負である条件
このパターンは非常に簡単で、端点の条件 1 つだけで解決します。
- 端点： f(0)<0
- x=0 で y 座標が負（x 軸との交点が x 軸より下）にあることを確認するだけです。
【なぜ f(0)<0 だけでいいのか？】 下に凸のグラフを考えた場合、f(0)<0 の条件を満たす、つまり y 軸との交点が x 軸より下にあれば、グラフは必ずどこかで x 軸を突き破って左右に広がらざるを得ません。この瞬間、「必ず異なる2つの実数解を持つ」ことが確定し、D>0 となり、軸がどこにあっても「解が左右に一つずつある」状態が自動的に満たされてしまうため、他の条件を考える必要がなくなります。
例題（アウトプット）
問題 1：最大値・最小値（定義域が固定されたパターン）
二次関数 y=x^2−4x+5 について、定義域が 0≤x≤3 のとき、最大値と最小値を求めなさい。
問題 2：解の配置問題
二次方程式 x^2−2(a+1)x+4a=0 が、異なる 2 つの正の解を持つような定数 a の値の範囲を求めなさい。
解説
問題 1：最大値・最小値
まず、問題文に書かれている数式のグラフをイメージすることが大事です。
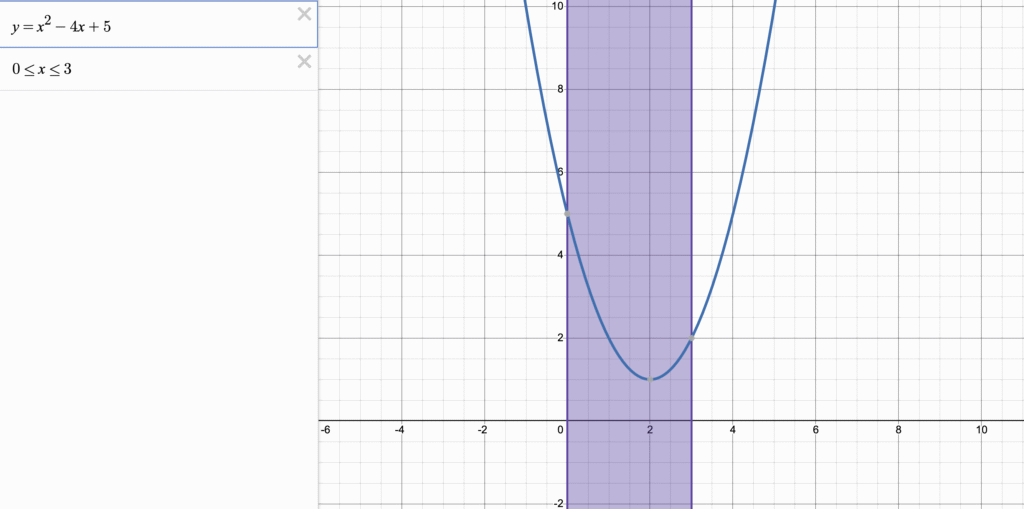
紫のところは定義域を表しています。このグラフをみると、「あ、下に凸のグラフなんだな」ということがわかります。そして、解くために必要なのは、平方完成ですね。平方完成で、頂点の座標、そして軸を求めることができるんでした。
平方完成したら、このような形になります。
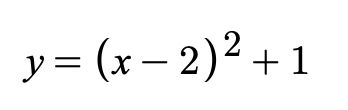
つまり、頂点が(2,1)であることがわかります。その次に定義域を見ます。そうすると、頂点の座標が定義域の中にありますね。なので、最小値はx=2の時、y=1であることがわかります。
そして、軸からどのくらい離れているかを見てみましょう。
x=2からx=0の方が遠いですよね。なので、最大値はx=0の時のy=5が最大値であることがわかります。
やはり重要なのは「軸」
軸を中心に考えていくことによって、答えを導き出すことができます。
問題 2：解の配置問題
「異なる 2 つの正の解」という条件というのは、軸の正の部分で2点交わるように、【端点・軸・判別式】の3つの条件を設定することで解くことができます。
判別式 D>0 （異なる2つの解を持つ）
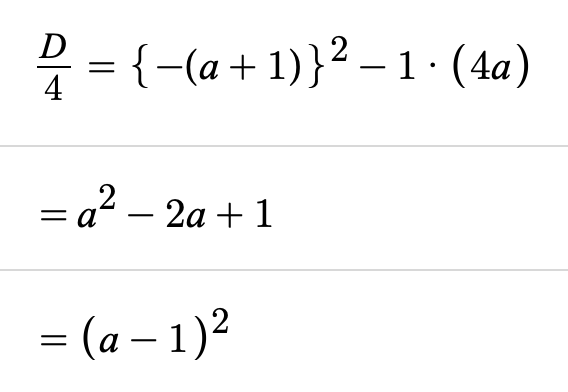
D>0になるのが条件でした。なので、a=1になってしまうと、（ ）の中が0になってしまうので、a=1にはならない…①ということが判別式からわかります。
2. 軸 >0 （軸が y 軸の右側にある）
軸を求めるのに必要な公式はなんだったでしょうか。
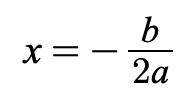
この式でしたね。この式に、aの値とbの値を代入します。注意すべきは、xの前の係数を全部をa,bと捉えることです。そして代入すると、
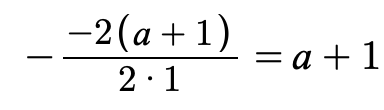
つまり、a+1が0にはなってはいけないので、aは-1よりも大きくなる。数式で表すと a>-1…② となります。
3. 端点 f(0)>0 （y 切片が x 軸より上にある）
そして端点です。x軸よりも上にあるので0以上ですね。なので、f(0)を代入します。
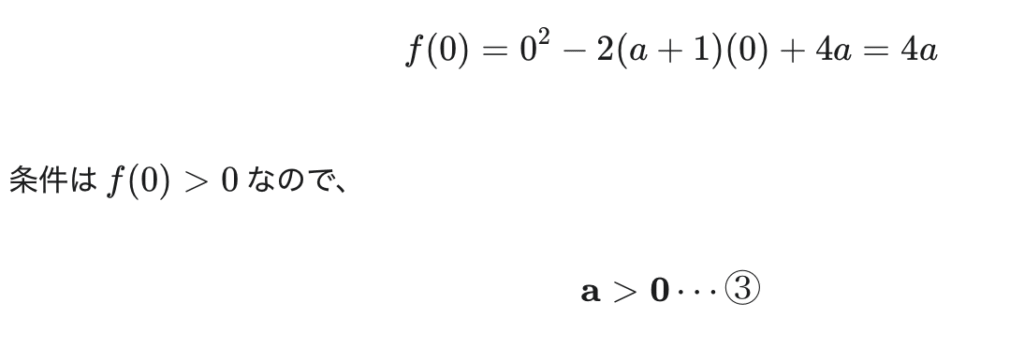
こうなりますね。
全ての条件を満たすaの値を求める
これら3つの条件を満たすaの値を求めましょう。①、②、③より、aのとりうる範囲は
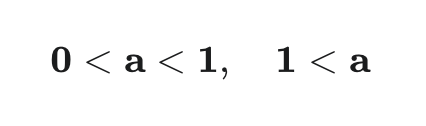
になります。これが問題2の答えです。
これらの例題のように、二次関数は「グラフのイメージ」、「軸」そして「条件を見つけて、それらを満たす値を見つける」を結びつける思考プロセスが最も重要です。何度も練習して二次関数を解けるようにしましょう。
コメント